Better Pricing: Part 1
This post is intended to document some of the ideas I have regarding the question of optimal pricing. The approach I take is rather academic and there are no immediate take-aways. I think of my ideas right now more as a a building block towards a more practical pricing solution.
Problem Set-up
Suppose you are owner of a car-sharing service with a single car type, i.e.we do not differentiate between multiple cars and once we decide on a price, it is applied to all cars simultaneously. You observe that the demand for cars differs over time (intra-day, intra-week, intra-month and intra-year). You also have some framework in place that predicts the expected demand in the next time frame.
In the following, we shall deal with time intervals, which can be as small as a few hours or as large as a few days. We shall stay agnostic to that in this post.
How do I even define Dynamic Pricing?
In this context of this post, we shall stick to the following definition:
Dynamic pricing is a demand-differentiated pricing policy aimed at achieving a certain revenue uplift by choosing higher pricer points for time frames with higher demand and vice versa.
Essentially, this pricing policy is a mapping between the expected demand and the price point that should be set.
Solution Design
The solution I am presenting here is an abstract proof-of-concept of the general idea, and for now I shall rely on the God’s intervention! Let me explain. The biggest problem one faces when designing a dynamic pricing solution is uncertainty. Above, I mentioned that we want to design a pricing policy that uses the expected demand to recommend a price. Where do we get the expected demand from?
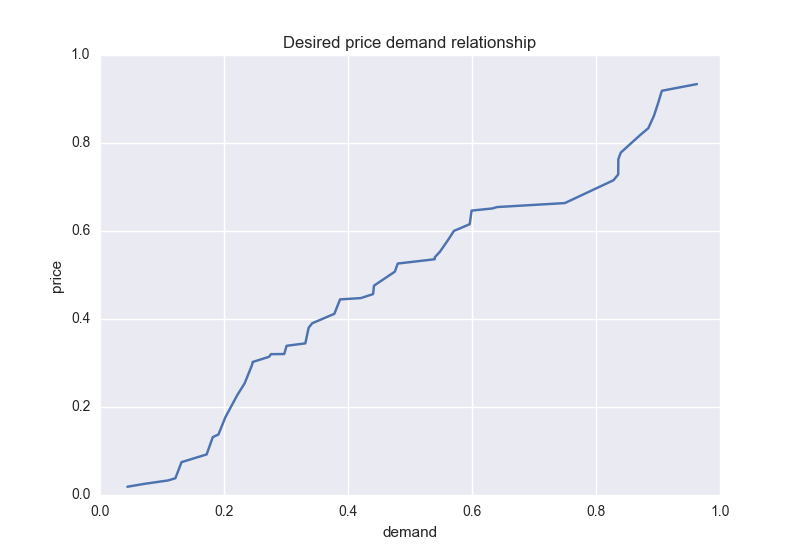
From here on, we are going to use the Word-of God (WoG) (really!) as a parameter to describe the solution. By WoG, I mean a floating point number between [0, 1], where the complete interval is mapped to a monotonically increasing demand function. Let’s call this f(x).
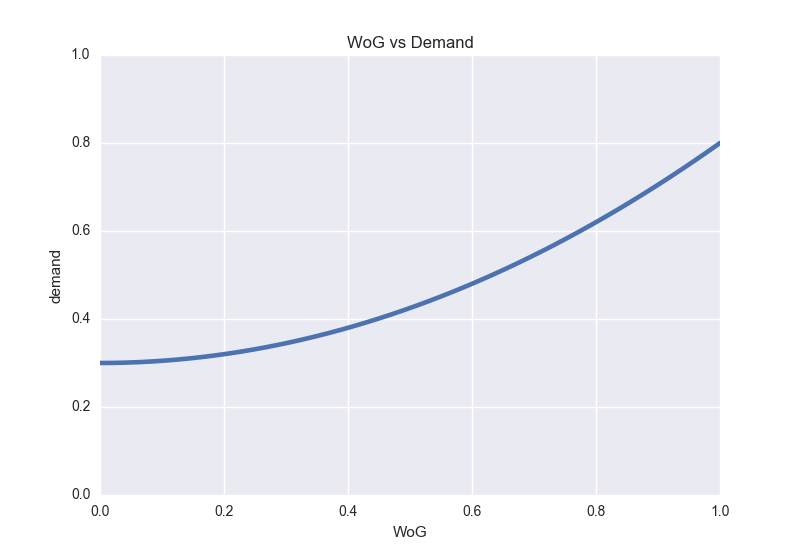
In other words, you use the Word-of-God, and use the above mapping to get the exact demand for the time interval under question. Next, we need to know the frequency distribution of WoG too. We assume this is available too. Let’s call this g(x).
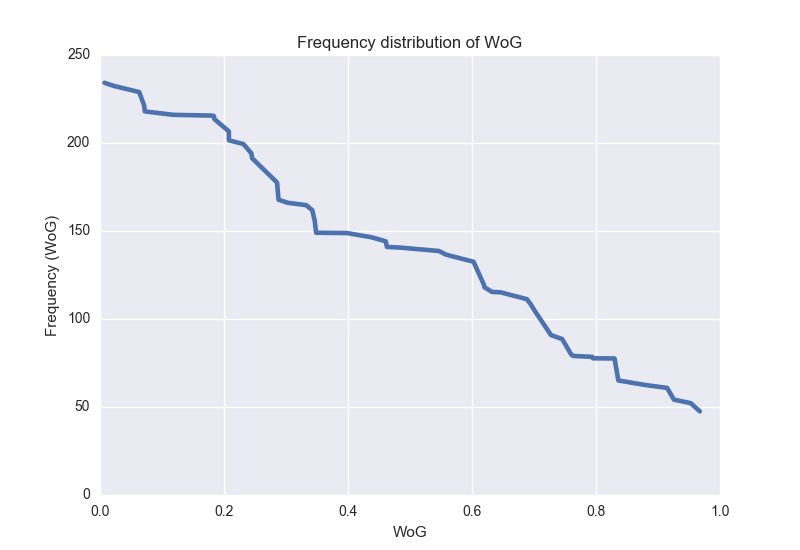
Note that the both the components described above are simply given to you and are not something you can influence. The last component is what we actually want to change. Given the WoG, what is the price point you choose? Let’s say, your current system looks as follows. Let’s call this h(x).
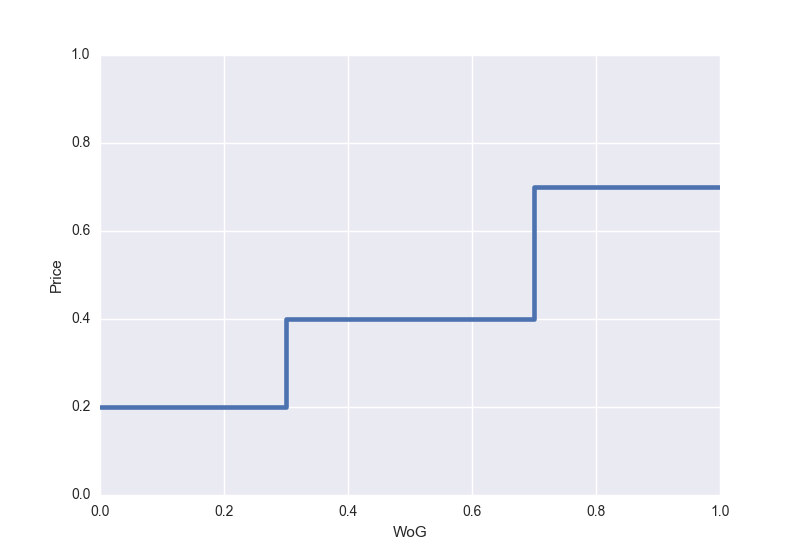
Notice that we can compute the current total revenue as follows:
\[\int\limits_{0}^{1} f(x)g(x)h(x) dx\]Constraints
To compute this new pricing policy, instead of focusing directly on the revenue, we shall use percentage change in ATP as constraint. Say, for example, that the percentage increase in ATP should be at most 5%. This means:
\[\frac{\sum_i (p_i^{new}- p_i^{old})}{\sum_i p_i^{old}} ~\leq~ 0.05\]Alternatively, we could write this constraint as:
\[\newcommand{\bm}[1]{\boldsymbol{#1}} \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \newcommand{\p}{\bm{p}} \newcommand{\x}{\bm{x}} \norm{\p^{new}} ~\leq~ 1.05 \cdot \norm{\p^{old}}\\\]where $\p^{new}$ and $\p^{old}$ denote the vector of new and old prices respectively and $\norm{\cdot}$ denotes the $\ell_1$ norm unless specified otherwise. This constraint ensures that sum of all prices do not increase by more than 5%. But there is nothing to stop the optimization algorithm from decreasing the prices for lower demand cases (alternatively, when WoG is close to 0) to 0 and that of increasing the price for higher demand cases to p_max. What we need is a regularization term.
In the next post, we shall look into what this regularization term should be, and what is the objective function we optimize. Before that a couple of comments:
- Note that in the current model, changes in price (for a given WoG value) has no impact whatsoever on the corresponding demand. In one of the subsequent posts, we shall address this issue.
- WoG is indeed an abstract concept. Think of it as being our prediction about a certain event (which is always accurate!).
